📗【算法】Princeton 算法课程 ② 栈和队列
栈和队列
- 栈:先进(入栈)后出(出栈)
- 队列:先进(入队)先出(出队)
在实现之前,老师提到了模块化的思想,它使得我们能够用模块式可复用的算法与数据结构的库来构建更复杂的算法和数据结构,也使我们能在必要的时候更关注效率。这门课也会严格遵守这种风格。
栈
假设我们有一个字符串的集合,我们想要实现对字符串集合的存储、定期取出并返回最后添加的字符串、检查集合是否为空。
下面是 API:

链表实现
课程中有关链表的操作都使用内部类定义节点元素:
private class Node {
String item;
Node next;
}
API 实现:
public class LinkedStackOfStrings {
private Node first = null;
private class Node {
String item;
Node next;
}
public boolean isEmpty() {
return first == null;
}
public void push (String item) {
Node oldfirst = first;
first = new Node();
first.item = item;
first.next = oldfirst;
}
public String pop() {
String item = first.item;
first = first.next;
return item;
}
}
上面的代码也体现了使用 Java 学习数据结构的优点,不需要考虑麻烦的指针,而且垃圾回收机制也避免了主动释放内存。
在实现中,每个操作的最坏时间需求都是常数的;在 Java 中,每个对象需要16字节的内存空间,在这里,内部类需要8字节,字符串和 Node 节点的引用也分别需要8字节,所以每个 Node 节点共需要40字节,当元素数量 N 很大时,40N 是对空间需求非常接近的估计。
数组实现
public class ResizingArrayStackOfStrings {
private String[] s;
private int N = 0;
public FixedCapacityStackOfStrings(int capacity) {
s = new String[capacity];
}
public boolean isEmpty() {
return N == 0;
}
public void push (String item) {
if (N == s.length)
resize(2 * s.length);
s[N++] = item;
}
public String pop() {
String item = s[--N];
s[N] = null;
if (N > 0 && N == s.length / 4)
resize(s.length / 2);
return item;
}
private void resize(int capacity) {
String[] copy = new String[capacity];
for (int i = 0; i < N; i++)
copy[i] = s[i];
s = copy;
}
public ResizingArrayStackOfStrings() {
s = new String[1];
}
}
平均运行时间还是与常数成正比,只不过进行内存分配时,需要 O(N) 的复杂度。
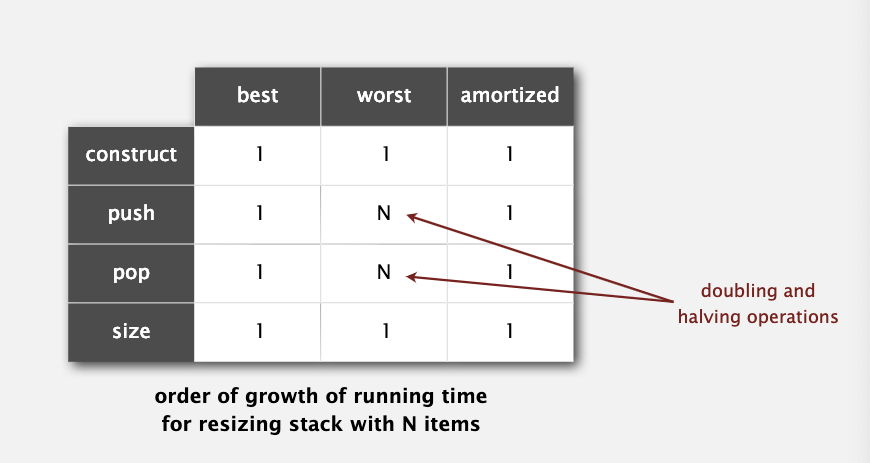
当栈慢时,内存空间为 sizeOf(int) * N = 8N 个字节;当栈的元素个数占总内存空间的 1/4 时,它包括 8 个 int 类型的地址,3*8N 个无用的空间,所以消耗内存 32N 个字节。
数组实现的栈内存占有在 8N 到 32N 之间。
动态数组 vs. 链表
虽然两种实现方式时间和空间复杂度近似相等,可还是有所差异。
在课程讨论区一位 mentor 就做过这样的解释。对于内存分析,链表耗内存的关键在于每个节点要存储两部分,假如说要存储32位的整数,那么链表实现要包含32位的整数和32位的地址,空间复杂度就是 O(64n bits);而数组只需要考虑一次开辟数组的内存,整个的内存消耗也就是 O(32n + 32 bits),虽然可以看做同一量级的复杂度,但实际上常数不一样,下面的网站可以很好地体现:
https://www.desmos.com/calculator/0gvfaytclt
时间复杂度链表要稳定一些,因为它每次操作都是 O(1),而数组虽然总体来讲要快一点,但可能需要 resize(),造成不稳定因素。老爷子也举例子说,如果要进行飞机降落,每一个环节都不能出错,或是数据传输,不能因为某一时刻速度减慢而造成丢包,那么使用链表是更好地选择。
队列
下面是队列的 API:

链表实现
public class LinkedQueueOfStrings {
private Node first, last;
private class Node {
String item;
Node next;
}
public boolean isEmpty() {
return first == null;
}
public void enqueue(String item) {
Node oldlast = last;
last = new Node();
last.item = item;
last.next = null;
if (isEmpty())
first = last;
else
oldlast.next = last;
}
public String dequeue() {
String item = first.item;
first = first.next;
if (isEmpty())
last = null;
return item;
}
}
泛型和迭代器
实现一个数据结构很自然要引入泛型,这里着重强调了 Java 不能创建泛型数组,所以使用强制转换来解决这一问题:
s = (Item[]) new Object[capacity];
虽然老爷子强调”A good code has zero cast”,不过这也是不得已而为之。
迭代器有利于数据结构的迭代,而且可以使用 Java 的 for-each 方法。下面是两种链表的 iterator 的实现:
public class Stack<Item> implements Iterable<Item> {
...
public Iterator<Item> iterator() {
return new ListIterator();
}
private class ListIterator implements Iterator<Item> {
private Node current = first;
public boolean hasNext() {
return current != null;
}
public void remove() {
/* not support */
}
public Item next() {
Item item = current.item;
current = current.next;
return item;
}
}
}
public class Stack<Item> implements Iterable<Item> {
...
public Iterator<Item> iterator() {
return new ReverseArrayIterator();
}
private class ReverseArrayIterator implements Iterator<Item> {
private int i = N;
public boolean hasNext() {
return i > 0;
}
public void remove() {
/* not support */
}
public Item next() {
return s[--i];
}
}
}
栈和队列的应用
其实讲的还是栈的应用,列举了下面几点:
- 编译器中的解析器
- Java 虚拟机
- word 中的撤销操作
- 浏览器中的后退键
- 函数调用
又详细讲了算数表达式求值的 Dijkstra 双栈算法。
初级排序
一开始讲了类实现 Comparable 接口的 compareTo() 方法,可以调用内置的 sort() 函数进行排序。
在排序算法的实现中,比较和交换是两种最基础的操作,下面是他们的代码实现:
private static boolean less(Comparable v, Comparable w) {
return v.conpareTo(w) < 0;
}
private static void exch(Comparable[]a, int i, int j) {
Comparable swap = a[i];
a[i] = a[j];
a[j] = swap;
}
选择排序
基本的选择排序的方法是在第 i 次迭代中,索引比 i 更大的项中找到最小的的一项,然后和第 i 项交换。
public static void sort(Comparable[] a) {
int N = a.length;
for (int i = 0; i < N; i++) {
int min = i;
for (int j = i + 1; j < N; j++)
if (less(a[j], a[min])
min = j;
exch(a, i, min);
}
}
选择排序使用了 (N-1) + (N-2) + … + 1 + 0 ~ (N^2 / 2) 次比较和 N 次交换。时间复杂度是 O(N^2) ;空间复杂度是 O(N)。
插入排序
对于第 i 个元素,将它与左边的元素比较,如果较小,则依次交换位置,直到被交换到正确的位置。
public static void sort(Comparable[] a) {
int N = a.length();
for (int i = 0; i < N; i++)
for (int j = i; j > 0; j--)
if (less(a[j], a[j-1]))
exch(a, j, j - 1);
else
break;
}
插入排序需要使用大约 1/4 N^2 次比较和大约 1/4 N^2 次交换,对于部分有序的数组,它的时间复杂度是线性的。
希尔排序
希尔排序以插入排序为出发点,进行一些调整,插入排序影响效率的主要因素是每次只能与相邻的元素交换,希尔排序的思想在于每次将数组项移动若干位置,每次排序都是在上一次基础上进行的,所以只需要进行少数几次交换。
这里提出了一种手段,h-排序,即每次向前移动 h 个位置,其实 h = 1 时就是插入排序。希尔排序最关键的一步是找出递增序列(就是 h 的序列),进行序列中的 h-排序 后,数组应该保持有序,而且时间要尽量做到最优。我们使用的是 3x+1 的递增序列。
public static void sort(Comparable[] a) {
int N = a.length;
int h = 1;
while (h < N/3)
h = 3 * h + 1; // 1, 4, 13, 40, 121, 364, ...
while (h >= 1) {
// h-sort the array
for (int i = h; i < N; i++) {
for (int j = i; j >= h && less(a[j], a[j-h]); j -= h)
exch(a, j, j - h);
}
h = h / 3;
}
}
3x+1 序列下最差的比较次数是 O(N^{3/2}) ,不过实际上并没有那么慢,一般来讲时间复杂度大约是 O(NlogN)。简单的思想、不太复杂的代码,却带了显著的效率的提升,所以希尔排序一般用于嵌入式排序或硬件排序类的系统。
不过目前为止都不能找到一个更好的序列,能使希尔排序的效率高于其他的一些更复杂的经典算法。
编程作业
本周的作业是实现一个双端队列和一个随机队列。
因为要求中提到了每个方法最差要达到常数时间复杂度,所以毫无疑问使用链表实现,设置头结点和指向前节点的指针,便于逆序访问。
public class Deque<Item> implements Iterable<Item> {
private Node first;
private int size = 0;
private class Node {
Item value;
Node next;
Node prev;
}
/**
* construct an empty deque
*/
public Deque() {
first = new Node();
first.next = first;
first.prev = first;
}
/**
* is the deque empty?
* @return
*/
public boolean isEmpty() {
return size == 0;
}
/**
*
* @return the number of items on the queue
*/
public int size() {
return this.size;
}
/**
* add the item to the front
* @param item
*/
public void addFirst(Item item) {
if (item == null)
throw new IllegalArgumentException();
Node lastfirst = first.next;
first.next = new Node();
first.next.value = item;
first.next.next = lastfirst;
first.next.prev = first.next;
lastfirst.prev = first.next;
size++;
}
/**
* add the item to the last
* @param item
*/
public void addLast(Item item) {
if (item == null)
throw new IllegalArgumentException();
Node lastrear = first.prev;
first.prev = new Node();
first.prev.value = item;
first.prev.next = first;
first.prev.prev = lastrear;
lastrear.next = first.prev;
size++;
}
/**
* remove the item from the front
* @return
*/
public Item removeFirst() {
if (isEmpty())
throw new NoSuchElementException();
Node nextfirst = first.next.next;
Item item = first.next.value;
first.next = nextfirst;
nextfirst.prev = first;
size--;
return item;
}
/**
* remove the item from the last
* @return
*/
public Item removeLast() {
if (isEmpty())
throw new NoSuchElementException();
Node nextlast = first.prev.prev;
Item item = first.prev.value;
first.prev = nextlast;
nextlast.next = first;
size--;
return item;
}
/**
* return an iterator over items in order from front to end
* @return
*/
@Override
public Iterator<Item> iterator() {
return new DequeList();
}
private class DequeList implements Iterator<Item> {
private Node current = first.next;
@Override
public boolean hasNext() {
return current.next != first.next;
}
@Override
public Item next() {
if (!hasNext())
throw new NoSuchElementException();
Item item = current.value;
current = current.next;
return item;
}
@Override
public void remove() {
throw new UnsupportedOperationException();
}
}
}
随机队列要求出队的元素是随机的,我使用的是数组实现,随机一个索引,如果索引即为最后一个元素,则将其删除,否则将索引的元素与最后一个元素交换位置,再将它删除。
public class RandomizedQueue<Item> implements Iterable<Item> {
private int index = 0;
private Item[] arr;
/**
* construct an empty randomized queue
*/
public RandomizedQueue() {
arr = (Item[]) new Object[1];
}
/**
* is the randomized queue empty?
* @return
*/
public boolean isEmpty() {
return index == 0;
}
/**
*
* @return the number of items on the randomized queue
*/
public int size() {
return index;
}
/**
* add the item
* @param item
*/
public void enqueue(Item item) {
if (item == null)
throw new IllegalArgumentException();
if (index == arr.length)
resize(arr.length * 2);
arr[index++] = item;
}
/**
* remove and return a random item
* @return
*/
public Item dequeue() {
if (isEmpty())
throw new NoSuchElementException();
int i = StdRandom.uniform(index);
Item item = arr[i];
if (i == index - 1) {
arr[--index] = null;
} else {
arr[i] = arr[--index];
arr[index] = null;
}
if (index > 0 && index == arr.length / 4)
resize(arr.length / 2);
return item;
}
/**
* return a random item (but do not remove it)
* @return
*/
public Item sample() {
if (isEmpty())
throw new NoSuchElementException();
int i = StdRandom.uniform(index);
return arr[i];
}
private void resize(int capacity) {
Item[] copy = (Item[]) new Object[capacity];
for (int i = 0; i < index; i++) {
copy[i] = arr[i];
}
arr = copy;
}
/**
* return an independent iterator over items in random order
* @return
*/
@Override
public Iterator<Item> iterator() {
return new RandomizedQueueList();
}
private class RandomizedQueueList implements Iterator<Item> {
private int i = 0;
@Override
public boolean hasNext() {
return i < index;
}
@Override
public Item next() {
if (!hasNext())
throw new NoSuchElementException();
return arr[i++];
}
@Override
public void remove() {
throw new UnsupportedOperationException();
}
}
}
- 版权声明:本文采用知识共享 3.0 许可证 (保持署名-自由转载-非商用-非衍生)
- 发表于 2019-04-02