📗【算法】Princeton 算法课程 ③ 归并排序和快速排序
归并排序
归并排序的思想是把数组一分为二,然后再不断将小数组递归地一分为二下去,经过一系列排序再将它们合并起来。
private static void merge(Comparable[] a, Comparable[] aux, int lo, int mid, int hi) {
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
int i = lo, j = mid + 1;
for (int k = lo; k <= hi; k++) {
if (i > mid)
a[k] = aux[j++];
else if (j > hi)
a[k] = aux[i++];
else if (less(aux[j], aux[i]))
a[k] = aux[j++];
else
a[k] = aux[i++];
}
}
private static void sort(Comparable[] a, Comparable[] aux, int lo, int hi) {
if (hi <= lo)
return;
int mid = lo + (hi - lo) / 2;
sort(a, aux, lo, mid);
sort(a, aux, mid+1, hi);
if(!less(a[mid + 1], a[mid]))
return;
merge(a, aux, lo, mid, hi);
}
public static void sort(Comparable[] a) {
Comparable[] aux = new Comparable[a.length];
sort(a, aux, 0, a.length - 1);
}
归并排序可用于大量数据的排序,对于 million 和 billion 级别的数据,插入排序难以完成的任务归并排序可能几分钟就完成了。
对于 N 个元素,归并排序最多需要 NlgN 次比较和 6NlgN 次对数组的访问,并且要使用 N 个空间的辅助数组。
自底向上的归并排序
我们将归并排序的过程倒过来看,先将数组分为 2 个元素并将所有组排序,再分为 4 个元素并将所有组排序,… ,直到完成排序。
public static void sort(Comparable[] a) {
int N = a.length;
aux = new Comparable[N];
for (int sz = 1; sz < N; sz = sz + sz)
for (int lo = 0; lo < N - sz; lo += sz + sz)
merge(a, lo, lo + sz - 1, Math.min(lo+sz+sz-1, N-1));
}
这是一个完全符合工业标准的代码,除了需要额外的存储空间。时间复杂度为 O(NlogN)。
排序规则
我们可以实现 Comparator 接口来为排序算法编写不同的排序规则,以插入排序为例:
public static void sort(Object[] a, Comparator comparator) {
int N = a.length;
for (int i = 0; i < N; i++)
for (int j = i; j > 0 && less(comparator, a[j], a[j-1]); j--)
exch(a, j, j - 1);
}
private static boolean less(Comparator c, Object v, Object w) {
return c.compare(v, m) < 0;
}
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
public class Student {
public static final Comparator<Student> BY_NAME = new ByName();
...
private static class ByName implements Comparator<Student> {
public int compare(Student v, Student w)
return v.name.compareTo(w.name);
}
}
然后可以这样使用排序:
Arrays.sort(a, Student.BY_NAME);
使用 Comparator 接口来替代 Comparable 接口的优点就是它支持待排序元素的多种排序规则。
快速排序
快速排序广泛运用于系统排序和其他应用中。它也是一个递归过程,与归并排序不同的是,它先进行操作然后再递归,而不是归并排序先进性递归然后再进行 merge。
算法的思想是先对数组随机打乱,然后每次都把第一个元素放到合适的位置,这个位置左边的元素都比它小,右边的元素都比它大,再将两侧的元素递归操作。
private static int partition(Comparable[] a, int lo, int hi) {
int i = lo, j = hi + 1;
while (true) {
while (less(a[++i], a[lo]))
if (i == hi)
break;
while (less(a[lo], a[--j]))
if (j == lo)
break;
if (i >= j)
break;
exch(a, i, j);
}
exch(a, lo, j);
return j;
}
public static void sort(Comparable[] a) {
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo)
return;
int j = partition(a, lo, hi);
sort(a, lo, j - 1);
sort(a, j + 1, hi);
}
事实证明,快速排序比归并排序还要快,他最少需要 NlgN 次比较,最多需要 1/2 N^2 次。对于 N 个元素,快速排序平均需要 1.39NlgN 次比较,不过因为不需要过多的元素的移动,所以实际上它更快一些。其中,随机打乱是为了避免最坏的情况。
在空间使用上,它不需要额外的空间,所以是常数级别的。
案例
快速排序的一个案例是找一个数组中第 k 大的数。
public static Comparable select(Comparable[] a, int k) {
StdRandom.shuffle(a);
int lo = 0, hi = a.length - 1;
while (hi > lo) {
int j = partition(a, lo, hi);
if (j < k)
lo = j + 1;
else if (j > k)
hi = j - 1;
else
return a[k];
}
return a[k];
}
这个解法的时间复杂度是线性的,不过有论文表明它的常数很大,所以在实践中效果不是特别好。
多个相同键值
很多时候排序的目的是将相同键值的元素排到一起,处理这种问题不同的排序方法的效率也不同。
归并排序需要 1/2 NlgN 至 NlgN 次比较。
快速排序将达到 N^2 除非 partition 过程停止的键值和结果键值相等,所以需要更好的算法实现.
比较好的一种算法是 Dijkstra 三向切分,它将数组分成了三个部分,是 Dijkstra 的荷兰国旗问题引发的一个思考,即使用三种不同的主键对数组进行排序。
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo)
return;
int lt = lo, gt = hi;
Comparable v = a[lo];
int i = lo;
while (i <= gt) {
int cmp = a[i].compareTo(v);
if (cmp < 0)
exch(a, lt++, i++);
else if (cmp > 0)
exch(a, i, gt--);
else
i++;
}
sort(a, lo, lt - 1);
sort(a, gt + 1, hi);
}
对于包含大量重复元素的数组,它将排序时间从线性对数级降低到了线性级别。
系统中的排序
Java 内置了一种排序方法——Arrays.sort(),这个方法使用两种排序方式共同实现。如果排序的是基本数据类型,就使用快速排序;如果排序的是对象,就使用归并排序。
因为对于基本类型来说快速排序会使用更少的空间,而且更快;而归并排序能保证 NlogN 的时间复杂度,而且更加稳定。
在视频的最后,老爷子强调对于不同的应用,要考虑的问题太多了,比如说并行、稳定等等,所以几乎每个重要的系统排序都有一个特定的高效算法,而且目前还有很多算法需要改进。
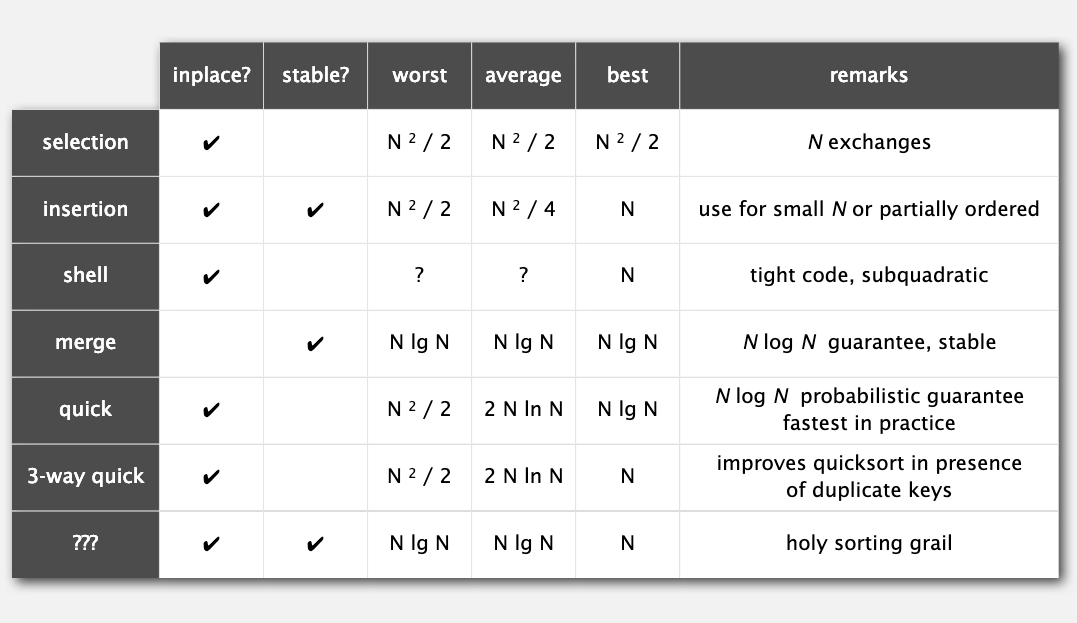
最后附上前面提到过的排序方法的总结:
编程作业:模式识别
给 n 个不同的点,找出所连线段,每条线段至少包括四个点。
首先补充完成 Point 类,这部分主要是练习使用 Comparable 和 Comparator 制定排序规则,具体的排序规则文档中有详细的描述。
public class Point implements Comparable<Point> {
private final int x; // x-coordinate of this point
private final int y; // y-coordinate of this point
/**
* Initializes a new point.
*
* @param x the <em>x</em>-coordinate of the point
* @param y the <em>y</em>-coordinate of the point
*/
public Point(int x, int y) {
/* DO NOT MODIFY */
this.x = x;
this.y = y;
}
/**
* Draws this point to standard draw.
*/
public void draw() {
/* DO NOT MODIFY */
StdDraw.point(x, y);
}
/**
* Draws the line segment between this point and the specified point
* to standard draw.
*
* @param that the other point
*/
public void drawTo(Point that) {
/* DO NOT MODIFY */
StdDraw.line(this.x, this.y, that.x, that.y);
}
/**
* Returns the slope between this point and the specified point.
* Formally, if the two points are (x0, y0) and (x1, y1), then the slope
* is (y1 - y0) / (x1 - x0). For completeness, the slope is defined to be
* +0.0 if the line segment connecting the two points is horizontal;
* Double.POSITIVE_INFINITY if the line segment is vertical;
* and Double.NEGATIVE_INFINITY if (x0, y0) and (x1, y1) are equal.
*
* @param that the other point
* @return the slope between this point and the specified point
*/
public double slopeTo(Point that) {
/* YOUR CODE HERE */
if (that == null)
throw new NoSuchElementException();
if (this.x == that.x && this.y == that.y)
return Double.NEGATIVE_INFINITY;
else if (this.x == that.x)
return Double.POSITIVE_INFINITY;
else if (this.y == that.y)
return +0;
else
return (this.y - that.y) * 1.0 / (this.x - that.x);
}
/**
* Compares two points by y-coordinate, breaking ties by x-coordinate.
* Formally, the invoking point (x0, y0) is less than the argument point
* (x1, y1) if and only if either y0 < y1 or if y0 = y1 and x0 < x1.
*
* @param that the other point
* @return the value <tt>0</tt> if this point is equal to the argument
* point (x0 = x1 and y0 = y1);
* a negative integer if this point is less than the argument
* point; and a positive integer if this point is greater than the
* argument point
*/
public int compareTo(Point that) {
/* YOUR CODE HERE */
if (that == null)
throw new NoSuchElementException();
if (this.x == that.x && this.y == that.y)
return 0;
if (this.y < that.y || (this.y == that.y && this.x < that.x))
return -1;
return 1;
}
/**
* Compares two points by the slope they make with this point.
* The slope is defined as in the slopeTo() method.
*
* @return the Comparator that defines this ordering on points
*/
public Comparator<Point> slopeOrder() {
/* YOUR CODE HERE */
return new SlopeCompare();
}
private class SlopeCompare implements Comparator<Point> {
@Override
public int compare(Point o1, Point o2) {
if (o1 == null || o2 == null)
throw new NoSuchElementException();
if (slopeTo(o1) == Double.NEGATIVE_INFINITY && slopeTo(o2) == Double.NEGATIVE_INFINITY)
return 0;
else if (slopeTo(o1) == Double.POSITIVE_INFINITY && slopeTo(o2) == Double.POSITIVE_INFINITY)
return 0;
else if (slopeTo(o1) == Double.POSITIVE_INFINITY && slopeTo(o2) == Double.NEGATIVE_INFINITY)
return 1;
else if (slopeTo(o1) == Double.NEGATIVE_INFINITY && slopeTo(o2) == Double.POSITIVE_INFINITY)
return -1;
else if (slopeTo(o1) - slopeTo(o2) > 0)
return 1;
else if (slopeTo(o1) - slopeTo(o2) < 0)
return -1;
// return slopeTo(o1) - slopeTo(o2) < 0 ? -1 : 1;
return 0;
}
}
/**
* Returns a string representation of this point.
* This method is provide for debugging;
* your program should not rely on the format of the string representation.
*
* @return a string representation of this point
*/
public String toString() {
/* DO NOT MODIFY */
return "(" + x + ", " + y + ")";
}
/**
* Unit tests the Point data type.
*/
public static void main(String[] args) {
/* YOUR CODE HERE */
Point p1 = new Point(0, 10);
Point p2 = new Point(10, 0);
System.out.println(p1.slopeTo(p2) == p2.slopeTo(p1));
Point p3 = new Point(0, 20);
System.out.println(p3.slopeOrder().compare(p1, p2));
}
}
然后根据给出的点求所能组成的线段,线段只包含四个点,由两端的点表示,这个方法是暴力方法,4次方的时间复杂度。
public class BruteCollinearPoints {
/** Record the linesegments */
private ArrayList<LineSegment> list;
/**
* find all line segments containing 4 points
* @param points
*/
public BruteCollinearPoints(Point[] points) {
if (points == null)
throw new IllegalArgumentException();
for (Point p : points) {
if (p == null)
throw new IllegalArgumentException();
}
for (int i = 0; i < points.length - 1; i++) {
for (int j = i + 1; j < points.length; j++) {
if (points[i].compareTo(points[j]) == 0)
throw new IllegalArgumentException();
}
}
list = new ArrayList<>();
int N = points.length;
for (int i = 0; i < N; i++) {
for (int j = i + 1; j < N; j++) {
for (int k = j + 1; k < N; k++) {
for (int t = k + 1; t < N; t++) {
if (points[i].slopeTo(points[j]) == points[i].slopeTo(points[k])
&& points[i].slopeTo(points[k]) == points[i].slopeTo(points[t]))
addLineSegment(points, i, j, k, t);
}
}
}
}
}
/**
* Add the line segment to list
* @param points
* @param i
* @param j
* @param k
* @param t
*/
private void addLineSegment(Point[] points, int i, int j, int k, int t) {
Point[] ps = new Point[]{points[i], points[j], points[k], points[t]};
Point min = ps[0], max = ps[0];
for (int index = 1; index < ps.length; index++) {
if (min.compareTo(ps[index]) > 0)
min = ps[index];
if (max.compareTo(ps[index]) < 0)
max = ps[index];
}
list.add(new LineSegment(min, max));
}
/**
* the number of line segments
* @return
*/
public int numberOfSegments() {
return list.size();
}
/**
* the line segments
* @return
*/
public LineSegment[] segments() {
LineSegment[] ans = new LineSegment[list.size()];
for (int i = 0; i < list.size(); i++) {
ans[i] = list.get(i);
}
return ans;
}
public static void main(String[] args) {
}
}
然后实现高效算法,这里就需要使用前面提到的比较规则,先使用快排将点集排序,取最小的点跟其他点的斜率比,如果达到四个点及以上斜率相同,则记录到数组中。
public class FastCollinearPoints {
/** Record the linesegments */
private ArrayList<LineSegment> list;
/**
* find all line segments containing 4 or more points
* @param points
*/
public FastCollinearPoints(Point[] points) {
if (points == null)
throw new IllegalArgumentException();
for (Point p : points) {
if (p == null)
throw new IllegalArgumentException();
}
for (int i = 0; i < points.length - 1; i++) {
for (int j = i + 1; j < points.length; j++) {
if (points[i].compareTo(points[j]) == 0)
throw new IllegalArgumentException();
}
}
list = new ArrayList<>();
int N = points.length;
Arrays.sort(points);
for (int i = 0; i < N - 1; i++) {
/** get the smallest point */
Arrays.sort(points);
Point min = points[i];
/** sort as the points' slope */
Arrays.sort(points, i, N, points[i].slopeOrder());
Point max = null;
int count = 0;
for (int j = i + 1; j < N - 1; j++) {
if (min.slopeTo(points[j]) == min.slopeTo(points[j + 1])) {
count++;
max = points[j + 1];
} else if (count != 2) {
count = 0;
}
if (count >= 2) {
count = 0;
list.add(new LineSegment(min, max));
}
}
}
}
/**
* the number of line segments
* @return
*/
public int numberOfSegments() {
return list.size();
}
/**
* the line segments
* @return
*/
public LineSegment[] segments() {
LineSegment[] ans = new LineSegment[list.size()];
for (int i = 0; i < list.size(); i++) {
ans[i] = list.get(i);
}
return ans;
}
public static void main(String[] args) {
In in = new In(args[0]);
int n = in.readInt();
Point[] points = new Point[n];
for (int i = 0; i < n; i++) {
int x = in.readInt();
int y = in.readInt();
points[i] = new Point(x, y);
}
StdDraw.enableDoubleBuffering();
StdDraw.setXscale(0, 32768);
StdDraw.setYscale(0, 32768);
for (Point p : points) {
p.draw();
}
StdDraw.show();
FastCollinearPoints collinear = new FastCollinearPoints(points);
for (LineSegment segment : collinear.segments()) {
StdOut.println(segment);
segment.draw();
}
StdDraw.show();
}
}
这次作业目前只拿了88分,应该对于大规模的数据仍有不足。
对了不得不说这门课的 PA 真的有趣:

- 版权声明:本文采用知识共享 3.0 许可证 (保持署名-自由转载-非商用-非衍生)
- 发表于 2019-04-25