📗【算法】Princeton 算法课程 ④ 优先队列和符号表
优先队列和符号表
优先队列在入队时与传统队列相同,而出队时可以指定规则,比如最大元素/最小元素出队等,下面是一个简单的 API:

二叉堆
二叉堆是堆有序的完全二叉树,键值存储在节点上,且父元素的键值比子元素的键值大。我们可以推测出最大的键值在根节点上,也就是 a[1](不使用数组的第一个位置)。
二叉堆实际存储在数组中,如果一个节点的索引是 k,那么它的父节点的索引是 k / 2, 子节点的索引是 2k 和 2k + 1。
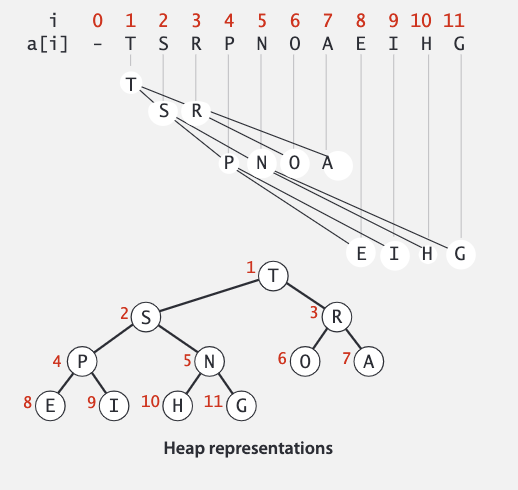
如果某一节点的堆有序被破坏了(子节点比父节点大),我们可以使用下面的算法恢复:
private void swim(int k) {
while (k > 1 && less(k / 2, k)) {
exch(k, k / 2);
k = k / 2;
}
}
因此实现添加操作时将待添加的元素插入到树的下一个子节点,然后通过 swim() 方法将其移动到正确的位置上,这个操作最多需要 1 + lgN 次比较。
public void insert(Key x) {
pq[++N] = x;
swim(N);
}
还有一种情况是父节点比两个子节点小,使用“下沉”的思想可以很好解决它:
private void sink(int k) {
while (2 * k <= N) {
int j = 2 * k;
if (j < N && less(j, j + 1))
j++;
if (!less(k, j))
break;
exch(k, j);
k = j;
}
}
sink() 方法利于实现删除操作,将首节点和尾节点互换位置,删除尾节点,再将首节点移动到合适的位置。这个操作最多需要 2lgN 次比较。
public Key delMax() {
Key max = pq[1];
exch(1, N--);
sink(1);
pq[N + 1] = null;
return max;
}
下面是完整的二叉堆的实现,这种实现的插入和删除操作都是 logN 的时间复杂度。
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq;
private int N;
public MaxPQ(int capacity) {
pq = (Key[]) new Comparable[capacity + 1];
}
public boolean isEmpty() {
return N == 0;
}
public void insert(Key key)
public Key delMax()
private void swim(int k)
private void sink(int k)
private boolean less(int i, int j) {
return pq[i].compareTo(pq[j]) < 0;
}
private void exch(int i, int j) {
Key t = pq[i];
pq[i] = pq[j];
pq[j] = t;
}
}
堆排序
堆排序分为两个阶段,第一个阶段是将数组安排到一个堆中,最好的方法是使用“下沉”操作,N 个元素只需要少于 2N 次比较和少于 N 次交换。
第二个阶段是通过二叉堆的删除方法,每次将二叉堆中最大的元素筛选出来,筛选出来的数组则是有序的。
public class Heap {
public static void sort(Comparable[] pq) {
int N = pq.length;
for (int k = N / 2; k >= 1; k--)
sink(a, k, N);
while (N > 1) {
exch(a, 1, N--);
sink(a, 1, N);
}
}
...
}
堆排序最多需要 2NlgN 次比较和交换操作,而且它是一个原地算法。
不过堆排序并不像想象中那么好,比如 Java 的 sort() 方法中就没有使用堆排序,它主要由以下三个缺点:
- 内循环太长
- 没能很好地利用缓存
- 不稳定
关于第二点,我一开始也不是很理解,后来 Google 除了答案。堆排序的过程中经常访问相距很远的元素,不利于缓存发挥作用;而快排等算法只会访问到局部的数据,因此缓存能更大概率命中,即局部性更强。
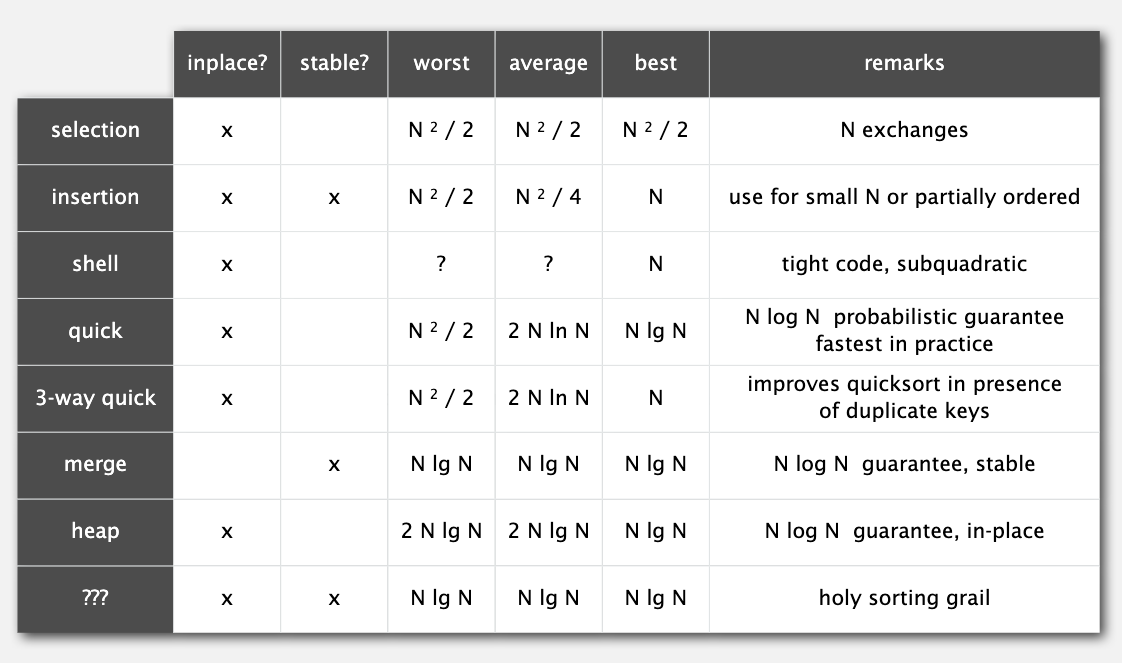
下面是截至目前所学排序算法的总结:
符号表
下面是符号表的 API。

位查找
实现符号表最简单的方法是使用链表,不过插入和查找操作都需要遍历整个链表,复杂度为 N。
因此我们可以使用两个数组实现,一个存储 key,一个存储 value,且存储是有序的。
public Value get(Key key) {
if (isEmpty())
return null;
int i = rank(key);
if (i < N && keys[i].compareTo(key) == 0)
return vals[i];
else
return null;
}
private int rank(Key key) {
int lo = 0, hi = N - 1;
while (lo <= hi) {
int mid = lo + (hi - lo) / 2;
int cmp = key.compareTo(keys[mid]);
if (cmp < 0)
hi = mid - 1;
else if (cmp > 0)
lo = mid + 1;
else
return mid;
}
return lo;
}
不过插入要移动数组元素。
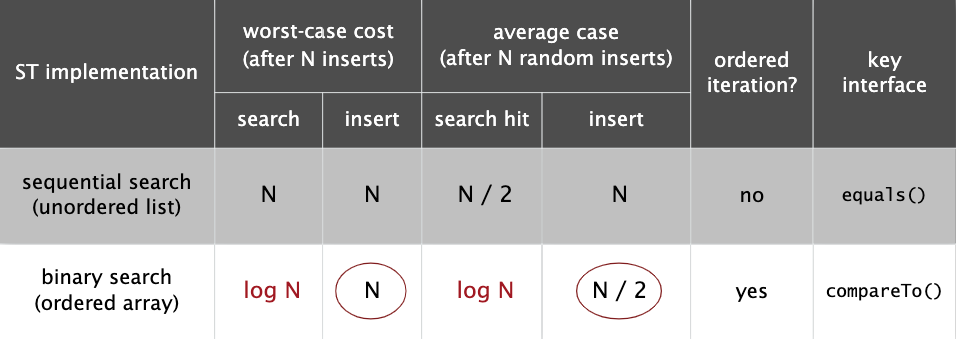
二分查找树
二分查找树实际上是一颗二叉树,节点上有值。父节点比所有左子节点上的元素大,比所有右子节点上的元素小。
public class BST<Key extends Comparable<Key>, Value> {
private Node root;
private class Node {
private Key key;
private Value val;
private Node left, right;
private int count;
public Node(Key key, Value val) {
this.key = key;
this.value = value;
}
}
public void put(Key key, Value val) {
root = put(root, key, val);
}
private Node put(Node x, Key key, Value val) {
if (x == null)
return new Node(key, val);
int cmp = key.compareTo(x.key);
if (cmp < 0)
x.left = put(x.left, key, val);
else if (cmp > 0)
x.right = put(x.right, key, val);
else
x.val = val;
x.count = 1 + size(x.left) + size(x.right);
return x;
}
public Value get(Key key) {
Node x = root;
while (x != null) {
int cmp = key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else
return x.val;
}
return null;
}
public int size() {
return size(root);
}
private int size(Node x) {
if (x == null)
return 0;
return x.count;
}
public Key min() {
return min(root).key;
}
private Node min(Node x) {
if (x.left == null)
return x;
return min(x.left);
}
public Key floor(Key key) {
Node x = floor(root, key);
if (x == null)
return null;
return x.key;
}
private Node floor(Node x, Key key) {
if (x == null)
return null;
int cmp = key.compareTo(x.key);
if (cmp == 0)
return x;
if (cmp < 0)
return floor(x.left, key);
Node t = floor(x.right, key);
if (t != null)
return t;
else
return x;
}
/** How many keys < k */
public int rank(Key key) {
return rank(key, root);
}
private int rank(Key key, Node x) {
if (x == null)
return 0;
int cmp = key.compareTo(x.key);
if (cmp < 0)
return rank(key, x.left);
else if (cmp > 0)
return 1 + size(x.left) + rank(key, x.right);
else
return rank(x.left);
}
public Iterator<Key> keys() {
Queue<Key> q = new Queue<>();
inorder(root, q);
return q;
}
private void inorder(Node x, Queue<Key> q) {
if (x == null)
return;
inorder(x.left, q);
q.enqueue(x.key);
inorder(x.right, q);
}
public void deleteMin() {
root = deleteMin(root);
}
private Node deleteMin(Node x) {
if (x.left == null)
return x.right;
x.left = deleteMin(x.left);
x.count = 1 + size(x.left) + size(x.right);
return x;
}
public void delete(Key key) {
root = delete(root, key);
}
private Node delete(Node x, Key key) {
if (x == null)
return null;
int cmp = key.compareTo(x.key);
if (cmp < 0)
x.left = delete(x.left, key);
else if (cmp > 0)
x.right = delete(x.right, key);
else {
if (x.right == null)
return x.left;
if (x.left == null)
return x.right;
Node t = x;
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
x.count = size(x.left) + size(x.right) + 2;
return x;
}
}
BST 的效率跟插入元素的顺序有关,最差的情况是所有节点都在其父节点的右子树上。
下面是二叉查找树各方法的效率:
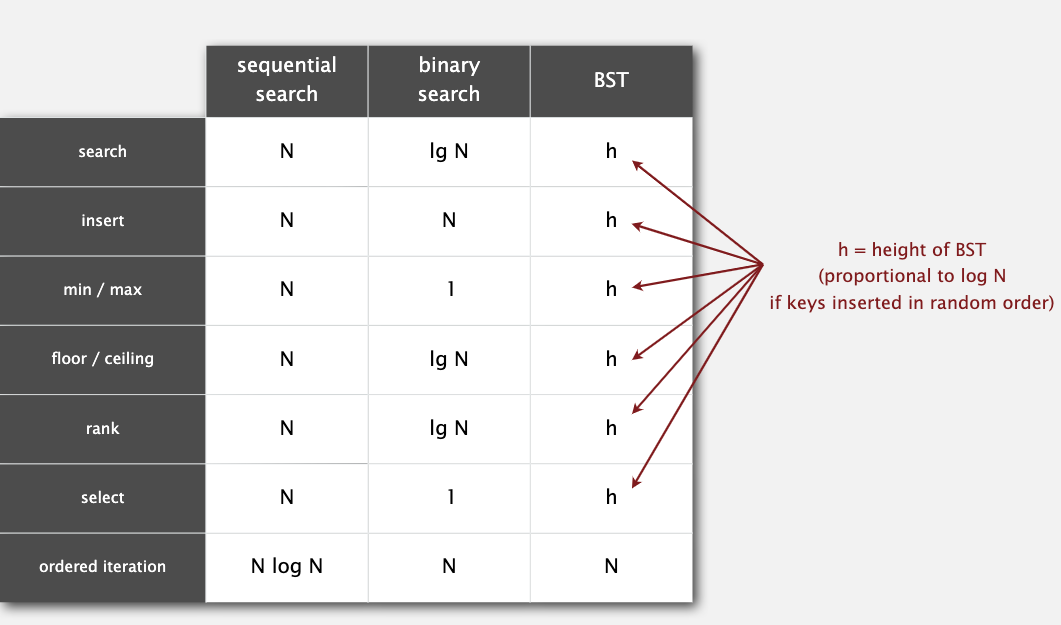
下面是二叉查找树与之前数据结构的对比:
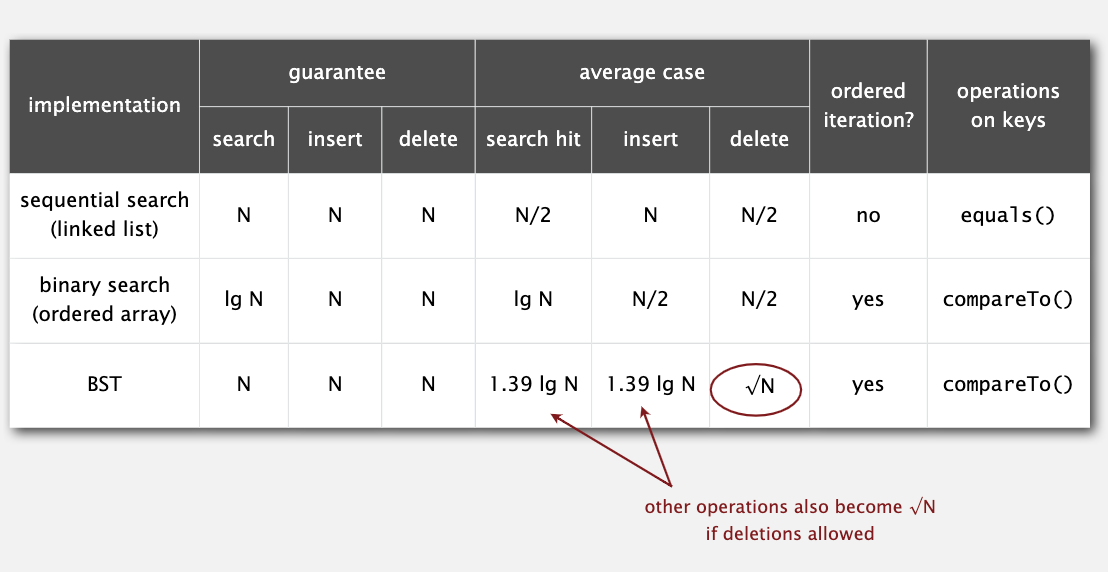
它的删除算法不算好,树的形状很容易偏向一侧,至今都没有什么好的解决办法。
编程作业:8 Puzzle
本次的作业是写一个游戏 AI,游戏即将一个无序的矩阵通过空白格的交换达到有序,如下图所示:
1 3 1 3 1 2 3 1 2 3 1 2 3
4 2 5 => 4 2 5 => 4 5 => 4 5 => 4 5 6
7 8 6 7 8 6 7 8 6 7 8 6 7 8
initial 1 left 2 up 5 left goal
讲真这次的作业做了好久好久,主要是不理解一开始给出的算法,只能硬着头皮边实现 API 边理解文档,最后调 bug 又调了两个小时,总之感觉是目前接触到最难得一次吧。
解决整个问题最核心的是 A* search 算法。每个矩阵都看作是一个搜索节点,一开始在 MinPQ 中插入所给的节点,然后删除最小的节点,并将最小节点的所有移动方法再插入到优先队列中,重复上述操作,直到队列中的最小节点有序。
所谓最小,即整个矩阵的复杂度最小,有 Hamming 和 Manhattan 两种优先度算法。两种方法都要经过测试,不过真正实现的时候要用 Manhattan 算法。
A* search 算法的操作可以想象成一棵博弈树,为了最终找到操作的过程,每个子节点还要存有父节点的引用。
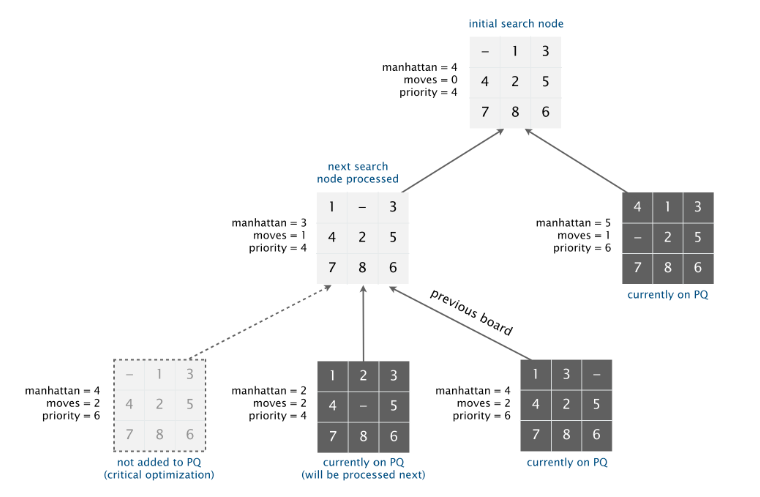
还要考虑的一种情况是,所给的矩阵根本无法调整为有序。这里的算法一直都不是很懂,一开始将原始节点的两个位置互换创建伴随节点啊,然后进行和原始节点相同的操作,如果原始节点无解的话,那么伴随节点一定有解。有兴趣的可以看一下这篇论文,给出了算法的证明。
大致梳理了一下思路后,就没有什么难懂的地方了。
Board 类主要就是记录输入数据,并实现比较规则以及一些生成方法供后续使用。
public class Board {
private final char[] blocks;
private final int n;
private int blankPos;
/**
* construct a board from an n-by-n array of blocks
* @param blocks
*/
public Board(int[][] blocks) {
if (blocks == null || blocks[0] == null)
throw new NullPointerException();
this.n = blocks.length;
this.blocks = new char[n * n + 1];
// 二维转一维
int index = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
this.blocks[++index] = (char) blocks[i][j];
if (this.blocks[index] == 0)
this.blankPos = index;
}
}
}
/**
* board dimension n
* @return
*/
public int dimension() {
return this.n;
}
/**
* number of blocks out of place
* @return
*/
public int hamming() {
int count = 0, index = 0;
for (int i = 1; i < blocks.length; i++) {
index++;
if (blocks[index] != i && blocks[index] != 0)
count++;
}
return count;
}
/**
* sum of Manhattan distancces between blocks and goal
* @return
*/
public int manhattan() {
int count = 0, index = 0;
for (int k = 1; k < blocks.length; k++) {
int value = blocks[++index];
if (value != 0) {
int correctPositionX = value % n == 0 ? value / n : value / n + 1,
correctPositionY = (value % n == 0 ? n : value % n);
int currentPositionX = index % n == 0 ? index / n : index / n + 1,
currentPositionY = (index % n == 0 ? n : index % n);
count += Math.abs(correctPositionX - currentPositionX) +
Math.abs(correctPositionY - currentPositionY);
// System.out.println(
// "current:(" + currentPositionX + ", " + currentPositionY + ")" +
// "\tcorrect:(" + correctPositionX + ", " + correctPositionY + ")" +
// "\tvalue: "+ value + "\tcount: " + count
// );
}
}
return count;
}
/**
* is this board the goal board?
* @return
*/
public boolean isGoal() {
for (int i = 1; i < blocks.length - 2; i++)
if (blocks[i] > blocks[i + 1])
return false;
return true;
}
/**
* a board that is obtained by exchanging any pair of blocks
* @return
*/
public Board twin() {
int index1 = -1, index2 = -1;
if (blocks[1] != 0 && blocks[2] != 0) {
index1 = 1;
index2 = 2;
} else {
index1 = n + 1;
index2 = n + 2;
}
return new Board(exchangeTwoEle(index1, index2));
}
/**
* exchange two elements and transfer to int[][]
* @param index1
* @param index2
* @return
*/
private int[][] exchangeTwoEle(int index1, int index2) {
int[][] bs = new int[n][n];
int value1 = blocks[index1], value2 = blocks[index2];
int index = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
index++;
if (index == index1)
bs[i][j] = value2;
else if (index == index2)
bs[i][j] = value1;
else
bs[i][j] = blocks[index];
}
}
return bs;
}
/**
* does this board equal y?
* @param y
* @return
*/
public boolean equals(Object y) {
if (this == y)
return true;
if (y == null)
return false;
if (this.getClass() != y.getClass())
return false;
Board b = (Board) y;
if (!Arrays.equals(this.blocks, b.blocks))
return false;
if (this.n != b.n)
return false;
return true;
}
/**
* all neighboring boards
* @return
*/
public Iterable<Board> neighbors() {
Stack<Board> stack = new Stack<>();
int index = blankPos;
if (index > n) {
// up
stack.push(new Board(exchangeTwoEle(index, index - n)));
}
if (index + n <= n * n) {
// down
stack.push(new Board(exchangeTwoEle(index, index + n)));
}
if (index > 0 && (index - 1) % n != 0) {
// left
stack.push(new Board(exchangeTwoEle(index, index - 1)));
}
if (index < n * n && (index + 1) % n != 1) {
// right
stack.push(new Board(exchangeTwoEle(index, index + 1)));
}
return stack;
}
/**
* string representation of this board (in the output format sprcified below)
* @return
*/
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append(n + "\n");
for (int i = 1; i <= n * n; i++) {
sb.append(String.format("%2d ", (int) blocks[i]));
if (i % n == 0)
sb.append("\n");
}
return sb.toString();
}
}
Solver 类包含一个内部类,即搜索节点,它主要包括 Board 和移动次数等信息。构造函数实现了 A* search 算法,其余方法只是为了输出结果。
public class Solver {
private final MinPQ<SearchNode> minPQ;
private final MinPQ<SearchNode> twins;
private class SearchNode implements Comparable<SearchNode> {
private final Board board;
private final int moves;
private final int priority;
private final SearchNode prevSearchNode;
public SearchNode(Board board, int moves, SearchNode prevSearchNode) {
this.board = board;
this.moves = moves;
this.priority = board.manhattan() + moves;
this.prevSearchNode = prevSearchNode;
}
@Override
public int compareTo(SearchNode sn) {
return this.priority - sn.priority;
}
}
/**
* find a solution to the initial board (using the A* algorithm)
* @param initial
*/
public Solver(Board initial) {
if (initial == null)
throw new IllegalArgumentException();
this.minPQ = new MinPQ<>();
this.twins = new MinPQ<>();
minPQ.insert(new SearchNode(initial, 0, null));
twins.insert(new SearchNode(initial.twin(), 0, null));
/**
* 删最低,插相邻,重复,最后剩一个
*/
while (!minPQ.min().board.isGoal() && !twins.min().board.isGoal()) {
SearchNode minSearchNode = minPQ.delMin();
SearchNode minTwins = twins.delMin();
for (Board b : minSearchNode.board.neighbors()) {
if (minSearchNode.moves == 0 || !b.equals(minSearchNode.prevSearchNode.board))
minPQ.insert(new SearchNode(b, minSearchNode.moves + 1, minSearchNode));
}
for (Board b : minTwins.board.neighbors()) {
if (minTwins.moves == 0 || !b.equals(minTwins.prevSearchNode.board))
twins.insert(new SearchNode(b, minTwins.moves + 1, minTwins));
}
}
}
/**
* is the initial board solvable?
* @return
*/
public boolean isSolvable() {
if (minPQ.min().board.isGoal())
return true;
return false;
}
/**
* min number of moves to solve initial board; -1 if unsolvable
* @return
*/
public int moves() {
if (!isSolvable())
return -1;
return minPQ.min().moves;
}
/**
* sequence if boards in a shortest solution; null if unsolvable
* @return
*/
public Iterable<Board> solution() {
if (!isSolvable())
return null;
Stack<Board> stack = new Stack<>();
SearchNode current = minPQ.min();
while (current != null) {
stack.push(current.board);
current = current.prevSearchNode;
}
return stack;
}
}
讲义中提到的几点优化一定要完成,效率会提高不少。还有一定要注意 Board 的输出格式,我就是少了个空格曾经一度得零分十几分。
测试数据并不是很难,我本地 puzzle50 没跑出来不过提交似乎没测试这么大的数据。可见这个 Ai 的算法还是有局限性的,对于 4*4 以上的复杂情况很难算出来。
最后部分数据超内存得了 95 分,下面上图感受一下曾经崩溃的心理。
幸亏不罚时。
- 版权声明:本文采用知识共享 3.0 许可证 (保持署名-自由转载-非商用-非衍生)
- 发表于 2019-05-22